Version: 1.0
· Introduction
· Case study
· How to use?
· Copyright
· Authors
· References
· Download
Ingve Simonsen and Rémi Lazzari

R. Lazzari and I. Simonsen,
Granfilm: a software for calculating thin-layer dielectric properties and fresnel coefficients,
Thin Solid Films 419, 124 (2002).
Introduction
Since the pioneering work of Maxwell Garnett [1] and Mie [2] at the
turn of the century, there has been large scientific interest in the
optical properties of metallic clusters [3]. Their optical behavior
are driven to a large extent by the Mie excitations [3] which can be
viewed as surface plasmon-polaritons [4]. Nearly hundred years ago Mie
[3] derived an exact theory for the scattering of light from a free
standing spherical particle. If, for isolated clusters with simple
shapes, such as spheres or spheroids in vacuum, the exact solution of
the Maxwell equations is well known, the difficulty of a reliable
description of the optical properties of particles dramatically
increases for interacting particles of complex shapes, either in a
matrix or on a surface. Even though the Maxwell Garnett effective
medium theory and other such theories [5] have been quite successful
in tackling these questions, an accurate description of the
macroscopic optical properties of a collection of particles supported
on a substrate, such as the Fresnel coefficients (absorption,
reflection and transmission), requires a more sophisticated approach
that accounts correctly for the break of symmetry brought by the
substrate and for realistic cluster shape. Indeed for clusters
deposited on a surface, a quantitative description of the optical
properties of thin films is not only hampered by the interactions
between aggregates but also by the image interactions between the
latter and the substrate [6-9].
In order to handle this latter situation in an adequate way, Bedeaux and Vlieger [10-14] in the first half of the 1970's introduced a model valid for layers whose thickness are in the sub-wavelength regime. In this case, they introduced modified boundary conditions on the surface for the electromagnetic fields which depend on what they called integrated excess quantities. In the closure relation between these quantities, they introduced surface susceptibilities which govern completely the far field behavior of the electromagnetic fields and thus the Fresnel quantities. In this way, they get rid of the complex behavior of the field on the surface. This approach is really analogous to the model of Feibelmann [15] and Barrera [16] who applied these notions in the case of the electromagnetic jump at metallic surfaces. However, Bedeaux and Vlieger were mainly interested in the description of the optical properties of island layers. For such layer, the main quantity which is directly related to the surface susceptibilities is the island polarizability. For simple shape like truncated spheres or spheroids with an axis of revolution normal to the surface of the substrate, a model based on a multipole expansion of the electrical potential in the non retarded limit was developed [17-20]. A nice recent, detailed and pedagogical introduction to this fascinating field of optics can be found in the recent book: Optical properties of Surfaces (Imperial College Press, 2001) by D. Bedeaux and J. Vlieger [21]. The aim of the present web page is to give access to the softwares which englobes most of the models developped in [21]. This software package we have named -- GranFilm.
A case study: Ag deposit on an MgO substrate
|
|
|
|
Fig 1: A scanning electron micrography of an Ag deposit on MgO obtained by vapor deposition (equivalent thickness 3nm). |
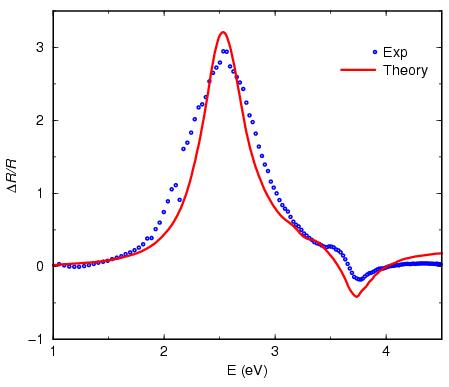
Fig. 2 : Comparison of the experimental and theoretical differential reflectivity curves. Consult Ref. [22,23] for details. |
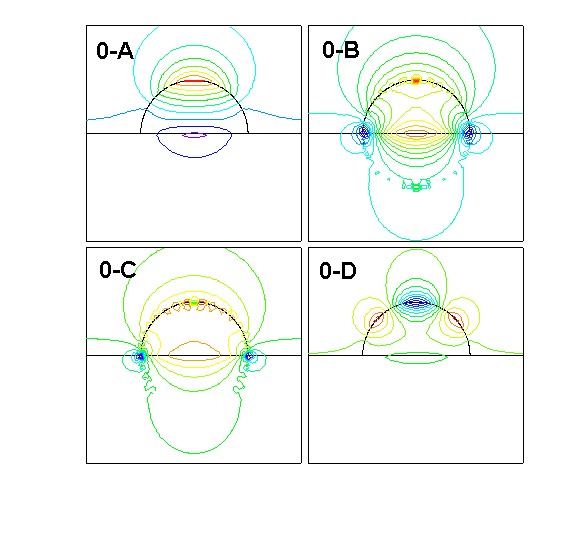
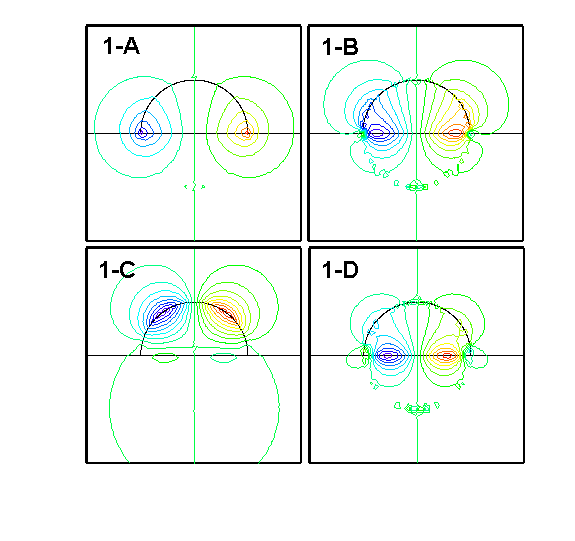
The solid red curve in Fig. 2 is a simulation result, obtained by using the GranFilm software. In obtaining these results, the islands were assumed to be approximated by truncated spheres of the same size and located on square grid (see [23] for details ). The island polarizability, which is the main ingredient in the calculations, was derived from a multipolar expansion of the potential with the image charge technique which allowed to account correctly for the coupling with the substrate and for the island shape through the fulfillment of the boundary conditions. The two main resonances in Fig. 2 are associated, in a first approximation, to the excitation of dipoles perpendicular and parallel to the substrate by the two components of the electric field. These modes, are depicted in Fig. 3 (0-A and 1-A, respectivley) by the polarization charges computed in the limit of small damping through the equipotential lines. Moreover, other multipolar modes (essentially of quadrupolar order) can be excited by the incident light thank to the special considered geometry.
|
|
|
| Fig 3 : Equipotential maps for the eigenmodes of the charge polarization for a truncated sphere. Notice the two types of modes which can be excited by the normal component of the electric field (left panel) and by the parallel one (right panel) (from [25]) | |
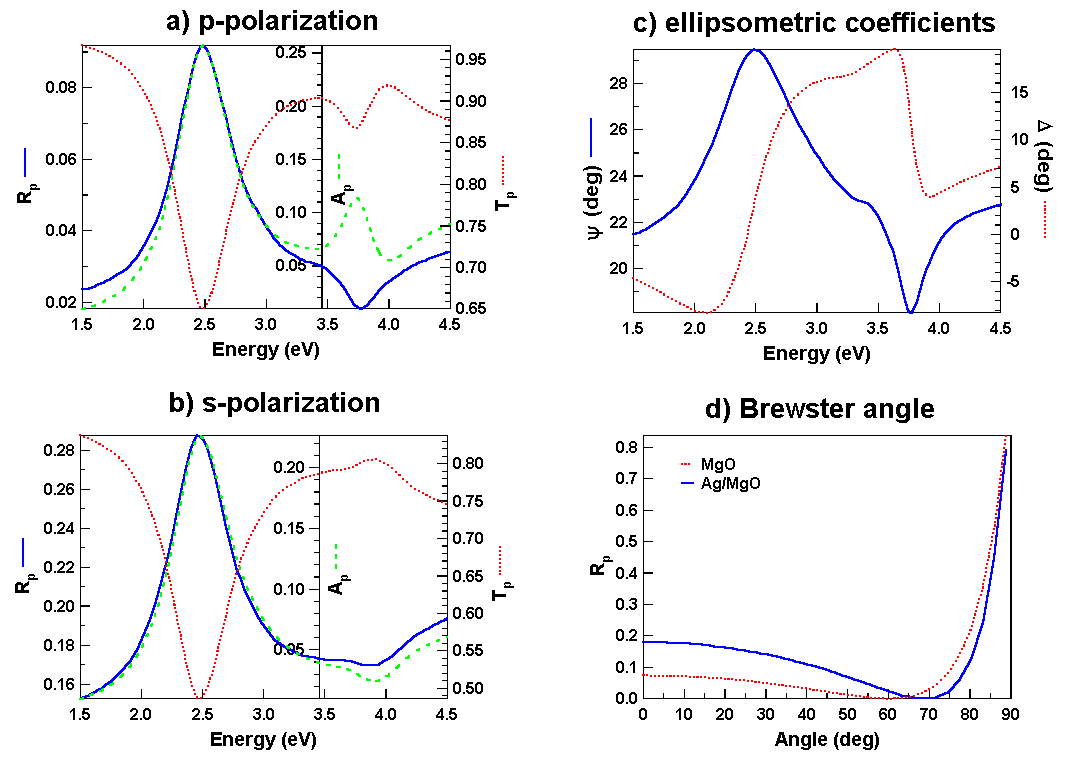
Of course GranFilm is capable of computing all the Fresnel coefficients once the island polarizability is known. An example of this is given in Fig. 4.
|
|
| Fig 4 : Computed Fresnel quantities (reflection, transmission, absorption and ellipsometric coefficients) for Ag islands on MgO (same parameters as for Fig. 2) (from [25]). |
The software
GranFilm is a software package aimed at calculating the polarizability of truncated spheres or spheroids deposited on a substrate as well as to calculate all the derived Fresnel quantities for island layers. It is suited for performing simulations for most of the models described in depth in the book Optical properties of Surfaces [21]. The implemented model account for the multipolar interaction of the particle with the substrate and for the coupling between clusters up to quadrupolar order. It as well includes simple dipole theory known as Yamaguchi model [6,7]. The software is written in the Fortran 90 programming language and has been extensively tested under the Linux and Windows 95/98/2000/NT operating systems. It should probably also work under other flavors of Unix as well as on the Mac OS, but this has not been tested. To compile the software from the provided source code, one will need the following libraries: Lapack, Slatec, FMZM and Pgplot. These libraries can be downloaded for free from the web by following the links. However, precompiled executable are provided for Linux and Windows which have these libraries statically linked (i.e. you do not need to have any of these libraries installed to run the software).
The installation and user instructions for GranFilm is provided in the ReadMe file that come with the distribution.
In order to use GranFilm, the user must provide the dielectric functions of both the metallic islands as well as the substrate. This information is located in files island.nk and substrate.nk respectively. They contain the index of refraction (n,k) of the material in two columns. The header of the file (first line) gives information about the abscissa axis : Unit(1=Energy in eV,2=Wavelenght in µm) – Start value – End value – Number of points. A dielectric database is furnished with the program and is taken from the free distribution by SOPRA corporation. Once launched the program automatically reads from the current directory a parameter file GranFilm.par which complies to your needs. For sphere and spheroid, they have slight different structures but contains more or less the same types of parameters. For example for a truncated sphere,Parameters | Possible values |
| Path to the dielectric constants files |
User defined (e.g. c: \Dielectric) |
| Geometry for the layer: either truncated sphere or thin continuous films |
|
|
Films thickness (nm) | User defined |
| Radius of the sphere (nm) Truncation value tr for the sphere Position of the multipole expansion µ | User defined User defined User defined (µ=0 is a good choice) |
| Type of clusters-clustesr interaction Type of lattice for the clusters (MFT=Mean Field Theory RPT=Renormalized Polarization theory) Lattice parameter (nm) Coverage (for MFT-RPT) |
none, dipole, quadrupole
User defined User defined |
| Computed Fresnel coefficient (Reflection, Differential Reflection, Transmission, Differential Transmission, Absorption) Polarization of the incident beam Incident angle (rad) Type of formulae for computing the Fresnel coefficient from the island polarizability | R, DR, T, DT, A p,s User defined constitutive, constitutive_all, invariants, aspnes |
|
Start energy (eV) End energy (eV) Number of points |
User defined User defined User defined |
|
Island or first film dielectric file (*.nk) Substrate dielectric file (*.nk) Second film dielectric file (*.nk) |
User defined User defined User defined |
|
Type of correction for the dielectric constant Correction for surface effect (Logical) |
none, finite_size, tau, manual, A-parameter, s-only T or F |
|
Output for the polarizability (Logical) Normalization of the polarizability by the island volume (Logical) Output for the multipolar coefficients (Logical) |
T or F T or F T or F |
| Type of calculation for the potential : none, the potential itself or fulfillment of the boundary condition on the sphere surface Energy (eV) where calculation is performed Type of normalization for the boundary conditions (BC) | None, Pot, BC User defined none, incident_field, mean_value |
| Number of multipoles in the expansion of the potential | User defined (less than 40 otherwise numerical limits are reached) |
|
Name of the ASCII output file (*.dat) | User defined |
| Comparison with experimental data of differential reflectivity (Logical) Name of the experimental file (*.dat) |
User defined |
For spheroid, the most different parameters are the following:
|
Parameters |
Possible values |
|
Type of calculation |
island, yamaguchi, coated |
|
Island radius parallel to the surface (nm) |
User defined |
|
Island radius perpendicular to the surface (nm) |
User defined |
|
Thickness of the coating (nm) |
User defined |
|
Coating dielectric constant |
User defined |
The coated geometry is that of a full spheroid coated by an overlayer and in dipolar interaction with the substrate [24].
To illustrate how the program works, the case described by the provided parameter file Sphere.inc corresponds to truncated silver spheres on-top of a dielectric (MgO) substrate. The main output from the simulations using this parameter file should be given as in the file SphereTest.dat. We have also provided as test case for the Spheroid program (Spheroid.inc and SpheroidTest.dat). Check that you can reproduce these results!
The authors are aware than these previous notice is succinct but with a close inspection of the literature, of the book Optical properties of Surfaces and of the program source codes, the user will undoubtedly be able to manage by himself. However, any comments, questions and suggestions are welcome.
GranFilm was developed by Ingve Simonsen and Rémi Lazzari. It is being released under the GNU General Public License and is provided as-is without any warranty. Any publication resulting from this software should acknowledge its use.|
Ingve Simonsen
Department of Physics Norwegian University of Science and Technology (NTNU) NO-7491 Trondheim NORWAY Office : +47 73 59 34 17 Fax : +47 73 59 77 Email : ingve.simonsen |
Rémi Lazzari
Institut des NanoSciences de Paris UMR7588, Boite Courrier 840 4 place Jussieu 75252 Paris Cedex 05 FRANCE Office : +33 (0)1 44 27 46 28 Fax : +33 (0)1 44 27 39 82 Email : remi.lazzari |
References
[1] J. C. Maxwell Garnett, Phil. Trans. Roy. Soc. London 203A, 385 (1904)
[3] G. Mie, Ann. Phys. 25, 377 (1908).
[3] U. Kreibig, Optical properties of metal clusters (Springer Verlag, 1995)
[4] J.D. Jackson, Classical Electrodynamics (John wiley and Sons, New York 1975)
[5] R. Landauer, in Proceedings of the First Conference on the Electromagnetic and Optical Properties of Inhomogeneous Media (AIP, New-York 1978)
[6] T. Yamaguchi, S. Yoshida and A. Kinbara, Thin Solid Films 18, 63 (1973)
[7] T. Yamaguchi, S. Yoshida and A. Kinbara, Thin Solid Films 21, 173 (1974)
[8] R.G. Barrera, M. del Castillo-Mussot and G. Monsivais, Phys. Rev. B 43,13879 (1991)
[9] C. Noguez and R.G. Barrera, Phys. Rev. B 57, 302 (1998)
[10] D. Bedeaux and J. Vlieger, Physica A 67, 55 (1973)
[11] D. Bedeaux and J. Vlieger, Physica A 73, 287 (1974)
[12] J. Vlieger and D. Bedeaux, Physica A 82, 221 (1976)
[13] D. Bedeaux and J. Vlieger, Thin Solid Films 69, 107 (1980)
[14] J. Vlieger and D. Bedeaux, Thin Solid Films 102, 265 (1983)
[15] P.J. Feibelman, Progress in Surface Science 12, 287 (1982)
[16] A. Bagchi, R.G. Barrera and R. Del Sole, Phys. Rev. B 20, 4824 (1979)
[17] M.M. Wind, J. Vlieger and D. Bedeaux, Physica A 141,133 (1987)
[18] M.M. Wind, P.A. Bobbert, J. Vlieger and D. Bedeaux, Physica A 143,164 (1987)
[19] M.M. Wind, P.A. Bobbert and J. Vlieger, Thin Solid Films 164, 57 (1988)
[20] M.T. Haarmans and D. Bedeaux, Thin solid Films 224, 117 (1993)
[21] D. Bedeaux and J. Vlieger, Optical properties of Surfaces (Imperial College Press, 2001) (Description of the book and how to order it)
[22] R. Lazzari, J. Jupille. and Y. Borensztein., Appl. Surf. Sci. 142, 451 (1999)
[23] I. Simonsen, R. Lazzari, J. Jupille, and S. Roux, Phys. Rev. B 61, 7722 (2000)
[24] C.F. Bohren and D.R. Huffman, Absorption and Scattering of Light by Small Particles (John Wiley and Sons, New York, 1983)
[25] R. Lazzari, Vers la maîtrise de la croissance de couches minces : une étude par spectroscopie optique et d'eacute;lectrosn, PhD Thesis – Paris XI - France
Download
Follow this link
in order to download GranFilm.
Number of hits since Dec 2001 :
Last modified: Thu Sep 15 18:20 2003